Monty Hall Problem Simulator

Problema Monty Hall este una dintre cele mai faimoase probleme matematice din domeniul Teoria probabilităților:

Într-un spectacol de jocuri de televiziune, gazda cere unui jucător să aleagă una din cele trei uși închise care se află în fața jucătorului. În spatele celor două uși sunt capre, iar în spatele unei uși este o mașină pe care jucătorul o poate câștiga atunci când a ales acea ușă. După ce jucătorul a selectat o ușă (care rămâne închisă), gazda deschide o altă ușă care are o capră în spatele ei. Gazdă îi întreabă pe jucător dacă vrea să stea la ușa pe care a ales-o la început sau dacă dorește să treacă la cealaltă ușă închisă.

Întrebarea este în mod evident: Dacă jucătorul trebuie să comute sau să stea pe ușa selectată?

Mulți oameni ar putea spune că nu contează dacă jucătorul comută ușa sau nu, deoarece probabilitatea de a câștiga mașina este 50/50 oricum. Chiar dacă acest lucru pare rezonabil deoarece există două uși identice închise, este un răspuns greșit.

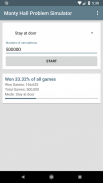
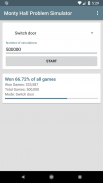
Răspunsul corect este că șansa de a câștiga mașina este de 67% atunci când jucătorul pornește ușa și doar 33% când jucătorul rămâne la ușa pe care a ales-o mai întâi.

Nu credeți că sa întâlnit încă? Doar descărcați aplicația și încercați!

Această aplicație vă permite să simulați automat scenariul de joc descris până la 5 milioane de ori la rând. Puteți alege dacă doriți ca jucătorul simulat să treacă mereu la ușă sau să stea întotdeauna la ușa pe care a ales-o mai întâi. După ce aplicația a simulat numărul de jocuri solicitate, vă oferă o statistică care vă arată câte dintre jocurile pe care le-a câștigat jucătorul. În acest fel puteți afla dacă playerul ar trebui sau nu ar trebui să comute ușa.